Bilangan Berakar

Pengertian Bilangan Berakar

 Bentuk akar adalah suatu bilangan irasional hasil pengakaran bilangan rasional. Bilangan rasional adalah bilangan yang bisa dibandingkan dengan bilangan lain dan biasanya berupa bilangan bulat, contohnya 2, 4, 16, 17, 21, dan sebagainya. 

Sementara itu, bilangan irasional adalah bilangan yang tidak berupa bilangan bulat dan tidak bisa dinyatakan sebagai pecahan, contoh 1,41; 2,17; 17,91; dan sebagainya.

Operasi bentuk ini merupakan kebalikan dari bilangan berpangkat, misalnya y=x²↔x=√y. Bentuk√y inilah yang disebut sebagai bentuk akar. Mengapa disebut demikian?

Karena bilangannya berada di dalam tanda akar (√). Cara membaca√y adalah “akar y”.

Contoh√y adalah√3, √5, √7, dan sebagainya. Berdasarkan pengertiannya, bentuk ini hanya diisi oleh bilangan yang hasil pengakarannya berupa bilangan irasional, misalnya√3 . Hasil dari√3 adalah 1,73205081.

Lantas, bagaimana dengan√36 ? Ternyata,√36 belum bisa dikatakan sebagai bentuk akar karena hasil pengakarannya tidak berupa bilangan irasional,√36 =6.

Nah, angka 6 merupakan bilangan rasional.

Sifat-Sifatnya

Adapun sifat-sifatnya adalah sebagai berikut.

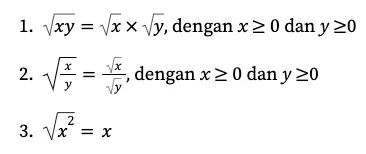
Operasi Bentuk Akar

Sama seperti bilangan bulat, bentuk akar juga bisa dioperasikan baik dengan bentuk akar lain maupun dengan bilangan real. Adapun operasinya adalah sebagai berikut.

1. Penjumlahan

Penjumlahan hanya bisa dilakukan jika angka yang berada di dalam tanda akar nilainya sama. Bentuk penjumlahannya adalah sebagai berikut.

p√x + q√x = (p+q)√x

Contoh:

• √2 + √2 = (1+1)√2=2√2
• 2√5 +3√5 = (2+3)√5=5√5

Penjumlahan tidak bisa dilakukan pada:

• Bentuk akar dan bilangan bulat biasa, misalnya, √2 + 2 ; dan
• Antarbentuk akar yang tidak sama bilangan pokoknya, misalnya√2 + √3.

2. Pengurangan

Konsep pengurangan sama seperti penjumlahan, yaitu hanya bisa dilakukan pada dua bentuk akar atau lebih yang bilangan pokoknya sama. Bentuk pengurangannya adalah sebagai berikut.

p√x – q√x = (p-q)√x

Contoh:

• 2√2 – √2 = (2-1)√2 = √2
• 2√5 – 3√5 = (2-3)√5 = –√5

3. Perkalian

Konsep perkalian bentuk ini berbeda dengan penjumlahan dan pengurangan. Hal itu karena perkalian bisa dilakukan antara bentuk akar dan bilangan nonakar, baik pecahan maupun bilangan bulat. Bentuk perkaliannya adalah sebagai berikut.

• p√x × q = (p×q)√x
• p√x × q√y = (p×q)√xy

Contoh perkaliannya adalah sebagai berikut.

• 4√7 × 2 = (4×2)√7 = 8√7
• √3 × 2√11 = (1×2)√33 = 2√33

3. Pembagian

Konsep pembagian, hampir sama dengan perkalian. Namun, pembagian bisa menghasilkan pecahan yang penyebutnya memuat bentuk akar. Jika berbentuk demikian, maka pecahan harus dirasionalkan penyebutnya. Adapun bentuk pembagiannya adalah sebagai berikut.

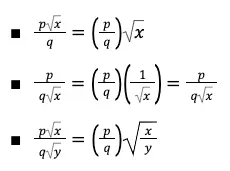
Contoh:

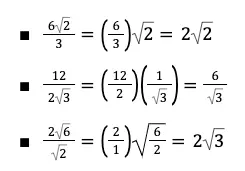
Cara Merasionalkan Bentuk Akar

Agar Quipperian semakin paham materi kali ini, yuk simak contoh soal berikut.

Contoh Soal 1

Pak Kusman memiliki kebun yang ukuran panjangnya (3√5 + √3) m dan lebarnya 2√3 m. Tentukan luas kebun Pak Kusman!

Pembahasan:

Diketahui:

p = 3√5 + √3 m

l = 2√3 m

Ditanya: L =…?

Penyelesaian:

Untuk mencari luas kebun Pak Kusman, Quipperian harus menggunakan operasi perkalian yang melibatkan bentuk akar.

L = p × l 

  = (3√5 + √3) × 2√3

= (3√5 x 2√3) + (√3 x 2√3)

 = (6√15 + 6) m²

Jadi, luas kebun Pak Kusman adalah (6√15 + 6) m².

Contoh Soal 2

Sebuah segitiga memiliki tinggi 2√2 cm. Jika luas segitiga tersebut 6 cm², tentukan panjang alasnya!

Pembahasan:

Diketahui:

t = 2√2 cm

L = 6 cm²

Ditanya: a =…?

Penyelesaian:

Untuk mencari panjang alas segitiga, Quipperian harus memahami konsep operasi pembagian beserta cara merasionalkan bentuk akar pada penyebutnya.

Jadi, panjang alas segitiga tersebut adalah 3√2 m.

Contoh Soal 3

Sebuah persegi memiliki luas alas 72 cm². Tentukan panjang sisi persegi tersebut!

Pembahasan:

Untuk mencari panjang sisi persegi, Quipperian harus memahami sifat-sifat perkalian pada bentuk akar.

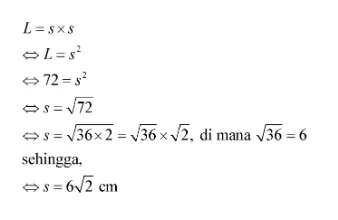
Jadi, panjang sisi perseginya adalah 6√2 cm.

sumber : https://www.quipper.com/id/blog/mapel/matematika/bentuk-akar/